Microhobby 11. Año II, del 15 al 21 de enero de 1985
Software: Manejo de los Gráficos Definidos por el Usuario
— Jesús Alonso
Para entender los «terribles» U.D.G. es necesario comprender primero la forma en la que trabaja la memoria del ordenador. Esperamos que tras la lectura de este artículo nadie tenga problemas en definir gráficos para sus propios programas.
A juzgar por las cartas recibidas en nuestra redacción, parece ser que uno de los principales problemas con que se encuentra el joven programador que se está iniciando en el BASIC, es la definición de U.D.G. (Gráficos Definidos por el Usuario). Este problema se debe, en la mayoría de los casos, al desconocimiento sobre la forma en que trabaja la memoria del ordenador. Para definir gráficos es indispensable utilizar el comando POKE que trabaja directamente sobre la memoria. Un gran número de lectores nos preguntan, también sobre la forma de utilizar este comando. Vamos a intentar, con este artículo, dar una explicación exhaustiva sobre la utilización del comando POKE y la definición de gráficos, para lo cual empezaremos por explicar cómo «cuenta» el ordenador.
Cómo «cuenta» el ordenador
Cuando nuestros remotos antepasados se plantearon el problema de numerar los objetos, decidieron en un principio, lo que parecía más evidente: utilizar los dedos de la mano. Hacían corresponder cada objeto con un dedo de la mano, y de esta forma, podían contar hasta cinco (de hecho nuestra palabra «contar» proviene de un vocablo griego que significa «hacer cinco»). Si utilizaban los dedos de ambas manos les era posible numerar un máximo de diez objetos. Posteriormente, los árabes idearon una serie de signos que se correspondían con los diez primeros números (del cero al nueve); el número con el que se correspondía cada signo venía dado por el número de ángulos que tuviera ese signo, así el cero era un círculo que, como sabemos, no tiene ningún ángulo; el uno era una figura con un ángulo; el dos tenía dos ángulos, y así sucesivamente hasta el nueve, que era una figura con nueve ángulos. Estos signos, ligeramente modificados, son los números que han llegado hasta nuestros días, por eso se les llama con frecuencia «Números arábigos».
Un sistema de numeración que sólo permita contar hasta nueve, no resulta demasiado útil, por otro lado no era cosa de inventar cien signos para contar hasta cien y luego pretender recordarlos todos, ¿se imagina el lector una figura con cien ángulos? Parecía mejor idea agrupar estos diez signos según una regla definida y obtener así cualquier número por grande que este fuera. Se pensó que los signos (también llamados dígitos) se colocarían en fila, el primero por la derecha representaría su valor multiplicado por uno, el segundo representaría su valor multiplicado por diez, el tercero, su valor por cien, y así sucesivamente, de esta forma el número 1984 significa: cuatro por uno más ocho por diez más nueve por cien más uno por mil. Pero uno, diez, cien y mil son potencias de diez (uno es diez elevado a cero, diez es diez elevado a uno, cien es diez elevado a dos, mil es diez elevado a tres, etc.), como se ve, los exponentes son los propios números, pero la base es siempre diez, por eso se llama a este sistema numeración decimal o de base diez. La base diez es tan común para nosotros que la creemos la única posible, pero de hecho se debe al accidente evolutivo de que tengamos diez dedos. No es la mejor base posible y existen otras. El BASIC es un lenguaje de programación ideado para que los humanos nos entendamos fácilmente con los ordenadores y por eso utiliza la base diez que es la más común para nosotros, pero el ordenador no tienen diez dedos y utiliza a nivel interno otra base de numeración que le resulta más fácil, la base dos.
Podemos imaginar la memoria de un ordenador como un tablero lleno de interruptores, cada uno de ellos puede estar «encendido» o «apagado». De forma arbitraria hacemos corresponder el estado «apagado» con el dígito «cero», y el estado «encendido» con el dígito «uno», con la posición de cada interruptor podemos numerar dos objetos, uno se llamaría «cero» y el otro se llamaría «uno», o lo que es lo mismo, podemos contar desde cero hasta uno. De nuevo, no resulta muy útil un sistema de numeración que sólo permita contar hasta uno. Vamos a hacer con nuestros interruptores lo mismo que los árabes con sus signos, vamos a agrupar nuestros interruptores. Supongamos que los agrupamos en filas de ocho interruptores (se pueden agrupar de cualquier otra forma, pero nuestro ordenador los agrupa de ocho en ocho). A cada interruptor lo llamamos «bit» y puede valer «cero» o «uno» según esté apagado o encendido, y al conjunto de ocho interruptores le llamamos «byte» o posición de memoria (a veces se le llama «palabra»), de esta forma estamos trabajando con «bytes» de ocho «bits» (los informáticos dicen «palabras de ocho bits»). El primer interruptor (bit) por la derecha, valdrá su valor multiplicado por uno (dos elevado a cero); el segundo, su valor multiplicado por dos (dos elevado a uno); el tercero, su valor multiplicado por cuatro (dos elevado a dos), y así hasta el último, que valdrá su valor multiplicado por 128 (dos elevado a siete). Vamos a situar nuestros ocho interruptores de forma que estén todos «encendidos». Nuestra posición de memoria contendrá el número 11111111 en binario (base dos), pero ese número también podemos expresarlo en base diez, será: uno por uno más uno por dos más uno por cuatro más uno por ocho más uno por 16 más uno por 32 más uno por 64 más uno por 128 igual a: 255. Este es el número decimal más alto que podemos escribir en nuestros ocho interruptores; si estuviesen todos apagados el número que contendrían sería «cero». Si ha entendido lo explicado hasta aquí, no debe tener problemas en calcular a qué número decimal corresponde la configuración de interruptores 11010010; si no es capaz de resolverlo, vuelva a leer otra vez todo el artículo.
Cuestión de ejercitarse
Bien, como ya habrá adivinado, el número decimal correspondiente es 210. Haga ejercicios con configuraciones diferentes hasta que domine el tema, y luego intente adivinar qué configuración de interruptores se corresponde con los números decimales: 24, 255, 60, 36, 66 y 129.
Si ha resuelto el ejercicio anterior, se encuentra usted en el camino de convertirse en un experto informático.
Supongamos, ahora, que tenemos un amigo en una fábrica de interruptores y nos regala todos los que queramos, así que cogemos una tabla muy grande y colocamos en ella 168 filas de ocho interruptores cada una, en total 1344 interruptores (tendremos que invitar un día a cenar a nuestro amigo). Ahora vamos a numerar las filas, a la primera fila la llamamos «cero», a la segunda la llamamos uno, y así sucesivamente hasta la última fila que se llamará 167. A estos números los llamamos «dirección», de modo que la dirección de la primera fila es «cero», la de la segunda es «uno», y así sucesivamente hasta la última, cuya dirección será 167. Al valor contenido en cada fila de interruptores lo llamamos «dato». Ahora tenemos lo que en informática se denomina una «memoria de 168 bytes con palabras de 8 bits». A un amigo nuestro le pedimos que introduzca en la dirección 37, el dato 210; él busca la fila de interruptores que hemos llamado «37» y los coloca en la configuración 11010010.
Cuando trabajamos con el ordenador, nuestro amigo se llama «intérprete de BASIC» y la forma de decirle que escriba el dato «210» en la dirección «37» sería: POKE 37, 210. De hecho, nuestro ordenador dispone de una «tabla» de 65536 filas de ocho interruptores cada una, pero los interruptores de las 16384 primeras filas están fijos, y no podemos alterar su configuración.
Quizá se pregunte usted cómo es posible que más de medio millón de interruptores quepan en un espacio tan reducido. La respuesta inmediata es que son muy pequeños. De hecho, no son interruptores pero se comportan como si lo fueran, y el suponer que son interruptores facilita la compresión y no afecta para nada a nuestro problema.
Almacenar en memoria
No parece muy útil almacenar datos en la memoria si luego no podemos hacer nada con ellos. Sin embargo, todo lo que hace el ordenador depende de los datos almacenados en su memoria. Incluso las letras que salen en la pantalla están guardadas en la memoria del ordenador, ya que de lo contrario, éste no sabría escribirlas. Las letra y signos que forman el juego de caracteres del ordenador no podemos alterarlos, ya que están guardados en las 16384 primeras filas de interruptores. Pero nuestro ordenador tiene prevista la posibilidad de que nosotros le definamos una serie de caracteres para que trabaje con ellos como si se tratara de los suyos propios. Estos son los U.D.G. o gráficos definidos por el usuario, son 21 y la información para escribirlos está contenida en 168 filas de «interruptores» que sí podemos alterar.
En primer lugar necesitamos saber en qué filas de interruptores (o más propiamente, «posiciones de memoria») almacena el ordenador estos gráficos, y a continuación, deberemos saber qué datos hay que introducir en estas posiciones de memoria para que el ordenador nos imprima un determinado gráfico que nosotros hayamos creado. Vamos en primer lugar con el primero de los problemas.
El ordenador procura siempre guardar esta información en la parte de la memoria donde menos estorbe, y, por supuesto, donde no pueda ser borrada por el BASIC. El lugar adecuado son, por tanto, las 168 últimas posiciones de la memoria. Como se verá, son distintas según se trate de un modelo de 16 ó de 48 K.
Las direcciones de estas posiciones de memoria son: de la 32600 a la 32767 para el modelo de 16K., y de la 65368 a la 65535 para el modelo de 48K. No se preocupe por tener que recordar estos números, ya que el ordenador los conoce, y nos los puede decir en cualquier momento si se lo sabemos preguntar. Cada carácter gráfico se almacena en ocho posiciones de memoria (por tanto, un carácter queda definido por los valores almacenados en 64 «interruptores»). La función USR «a» nos da la dirección de la primera de las posiciones de memoria correspondientes al gráfico definido por el usuario «a» (que es el primero de los U.D.G. y se obtiene con la «A» en modo gráfico). La función USR «b» nos dará la primera dirección del segundo gráfico, y así sucesivamente para los 21 gráficos posibles (hasta la «u»).
Datos a introducir
Ahora ya sabemos que para definir un gráfico tenemos que introducir ocho datos en memoria y las direcciones donde tenemos que introducirlos. Nos falta ser capaces de saber qué datos hay que introducir para generar un determinado gráfico.
Los gráficos que podemos generar han de ajustarse a un formato determinado, los haremos a base de puntos que estarán tan próximos que nos parecerán una figura. Cuantos más puntos utilicemos por unidad de superficie, más claramente se verá nuestra figura. La pantalla del Spectrum está compuesta por 45056 puntos (en informática se les llama «pixels») dispuestos en un rectángulo de 255 por 176 puntos (N.d.R: el dato sobre la medida de la pantalla es erróneo, el correcto es 256 por 192px). Cada punto está unido a un «interruptor» en la parte de la memoria denominada «archivo de presentación visual» (en inglés «display file»), podemos imaginarnos que cada punto es una bombilla que está iluminada cuando su correspondiente interruptor está encendido.
Cada segmento horizontal de ocho puntos está controlado por el dato almacenado en una determinada posición de memoria, y un conjunto de ocho segmentos colocados uno debajo de otro constituye un carácter que podrá ser una letra, un signo, o uno de nuestros gráficos U.D.G. (por cierto, U.D.G. son las iniciales de «User Defined Grafic», que en inglés significa «Gráfico Definido por el Usuario»).
Cuando el ordenador imprime un carácter, lo que hace es trasladar los datos que figuran en los ocho bytes de memoria que definen ese carácter a los ocho bytes correspondientes del archivo de presentación visual.
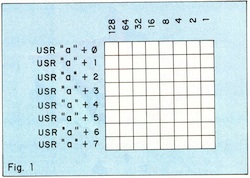
Como vemos, cada carácter sea letra, signo o U.D.G., se compone de 64 puntos agrupados en un cuadrado de ocho por ocho; así que, si vamos a generar nuestro propio gráfico, deberemos empezar por coger una hoja de papel cuadriculado. Dibuje en ella un cuadrado como el de la figura 1, que abarque ocho por ocho cuadritos.
A continuación sombreamos los cuadritos necesarios para que aparezca el gráfico que queremos definir, supongamos que queremos que al pulsar la tecla «A» en modo «gráfico», aparezca el hombrecito de la figura 2, así que sombrearemos los cuadritos correspondientes. Recuerde que no puede sombrear un cuadrito a medias, ya que cada cuadrito corresponde a un interruptor, y cada interruptor sólo puede estar «encendido» o «apagado»; un cuadrito sombreado corresponde a un interruptor «encendido» y un cuadrito en blanco, a uno apagado.
Seguro que ya ha adivinado que cada fila horizontal de ocho cuadritos corresponde a una fila de ocho interruptores, es decir, a un byte. Si ponemos un «cero» donde hay un cuadro en blanco, y un «uno» donde hay un cuadro sombreado, seremos capaces de calcular cuál es el dato decimal que debe contener cada una de las ocho filas de ocho interruptores.
| Dirección | Configuración binaria | Dato decimal |
|---|---|---|
| USR “a'+0 | 00011000 | 24 |
| USR “a”+1 | 00011000 | 24 |
| USR “a”+2 | 11111111 | 255 |
| USR “a”+3 | 00011000 | 24 |
| USR “a”+4 | 00011000 | 24 |
| USR “a”+5 | 00100100 | 36 |
| USR “a”+6 | 00100100 | 36 |
| USR “a”+7 | 00100100 | 36 |
En la primera columna «DIRECCIÓN», tenemos la forma de obtener las direcciones donde almacenar los datos de la columna «DATO DECIMAL»; la columna central «CONFIGURACION BINARIA», nos da una idea de cómo quedarían colocados nuestros 64 interruptores.
Para introducir esta información en memoria podríamos hacer:
10 POKE USR "a"+0,24 20 POKE USR "a"+1,24 30 POKE USR "a"+2,255 40 POKE USR "a"+3,24 50 POKE USR "a"+4,24 60 POKE USR "a"+5,36 70 POKE USR "a"+6,36 80 POKE USR "a"+7,36
Un método mejor
Pero este método ocupa mucha memoria y es lento de teclear, así que vamos a pensar un método mejor:
10 FOR n = 0 TO 7 20 READ dato 30 POKE USR "a" + n, dato 40 NEXT n 50 DATA 24, 24, 255, 24, 24, 36, 36, 36 60 PRINT AT 10, 10; CHR$ 144
Las cuatro primeras líneas introducen nuestros datos en memoria, la quinta contiene la lista de datos y, la sexta, nos imprime en pantalla el carácter gráfico que acabamos de generar.
Si desea que el gráfico salga al pulsar la tecla “B” en modo gráfico, cambie la línea 30 por POKE USR “b” + n,dato y la línea 60 por PRINT AT 10,10;CHR$ 145, de esta forma puede almacenar 21 caracteres gráficos en las letras de la “A” a la “U” que corresponde a los caracteres con códigos comprendidos entre 144 y 164.
Cuando se conecta el ordenador, estas posiciones contienen una copia de los correspondientes caracteres en mayúsculas, así que no se extrañe si al pulsar la “F” en modo gráfico sin haber definido un gráfico para la “F”, le sale precisamente una “F”, ¿qué otra cosa podía esperar?
Confiamos en que después de leer este artículo esté en disposición de generar maravillosos gráficos para adornar sus programas. Si desea gráficos más grandes, puede hacerlo agrupando varios gráficos pequeños como seguramente habrá visto en más de un programa comercial, esta es la versión particular del Spectrum de los famosos «Sprites».