Microhobby 25. Año II, del 23 al 29 de abril de 1985
Iniciación: Representación de los números en el Spectrum (I) Sistema binario
— José T. Crovetto
En la memoria del Spectrum toda la información se guarda en forma de «unos» y «ceros», es decir, como dígitos binarios o bits. Así pues, es necesario codificar en el alfabeto binario todos los símbolos a tratar. En esta serie de artículos veremos cómo se codifican los símbolos que representan cantidades numéricas. En primer lugar, vamos a familiarizarnos con los números enteros en notación binaria.
La forma habitual de trabajar con los números es la decimal o base diez. En esta base, manejamos diez cifras (del 0 al 9) y convenimos en representar los distintos números como combinaciones de estos diez dígitos decimales, a los cuales asignamos un peso según el lugar que ocupen dentro del número. Si comenzamos por la derecha, tenemos el dígito de las unidades, a su izquierda el de las decenas, centenas, etc. Es decir, el peso de cada uno de los dígitos decimales es la potencia de diez igual a la posición que ocupa, si comenzamos a contar desde cero y de derecha a izquierda. Por ejemplo, el número 974 decimal desglosado sería cuatro unidades (100= 1), siete decenas (101 = 10) y nueve centenas (102 = 100).
974 = 4 x 100 + 7 x 101 + 9 x 102 = 4 x 1 + 7 x 10 + 9 x 100
Veamos como este convenio, denominado representación polinomial, es igualmente aplicable a cualquier otra base y, en particular, a la base dos.
Representación en base 2
En base dos tenemos dos cifras (0 y 1) —el número de cifras es igual al valor decimal de la base—. Cualquier número expresado en este sistema se representa por combinaciones de los dígitos binarios, asignando un peso a cada uno de ellos según el lugar que ocupen. Así, el peso de cada uno de los bits que forman el número en notación binaria será la potencia de dos igual al lugar que ocupen, comenzando a contar desde cero y de derecha a izquierda. Por ejemplo, en el número binario 1010 los pesos de los distintos bits, comenzando por el de la derecha son: 20, 21, 22 y 23 respectivamente. La analogía con la base diez, a la que estamos acostumbrados, es completa.
Conviene que recordemos de memoria las ocho primeras potencias de dos, que se corresponden con los pesos de los ocho primeros bits de un número comenzando por el de la derecha (bit de menor peso).
| Potencias de 2 | |
|---|---|
| 20 = 1 | 24 = 16 |
| 21 = 2 | 25 = 32 |
| 22 = 4 | 26 = 64 |
| 23 = 8 | 27 = 128 |
Por ejemplo, el número en base dos 10011010 = 0 x 20 + 1 x 21 + 0 x 22 + 1 x 23 + 1 x 24 + 0 x 25 + 0 x 26 + 1 x 27 = 1 x 2 + 1 x 8 + 1 x 16 + 1 x 128 = 2 + 8 + 16 + 128 = 154 en base diez.
Como se ha visto en este ejemplo, en el que hemos convertido un número expresado en base dos a su equivalente en base diez, el método práctico y rápido de conversión de binario a decimal consiste en sumar los pesos de las posiciones en que haya «unos». El resultado es el equivalente en base diez.
Binario en el Spectrum
La operación de conversión de binario en decimal está resuelta en el Spectrum con el comando BIN. Pruebe el siguiente comando directo PRINT BIN 11111111 y el ordenador imprimirá en pantalla el número 255, que es su equivalente decimal. Efectivamente, puesto que el binario 11111111 = 1 x 20 + 1 X 21 + 1 X 22 + 1 X 23 + 1 X 24 + 1 x 25 1 x 26 + 1 x 27 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255 en base diez.
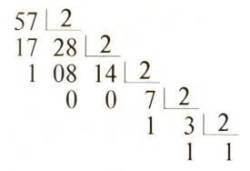
La operación inversa, es decir, dado un número en base diez calcular cual es su equivalente en base dos, no está implementada en el Spectrum. El método para esta conversión se denomina de divisiones sucesivas. Consiste en dividir el número entre dos y el cociente de esta división volver a dividirlo entre dos, y así sucesivamente hasta encontrar un cociente inferior a dos (es decir 1). Veamos un ejemplo: calculemos el equivalente binario del decimal 57:
Hemos puesto dentro de un círculo los restos de las divisiones y el último cociente. El equivalente binario se construye tomando estos números de abajo a arriba, es decir empezando por el último cociente, y escribiéndolos de izquierda a derecha. Entonces: 57D = 111001B. Convendremos en expresar la base en que se representa el número añadiendo al final de éste la letra mayúscula inicial de la base.
Obsérvese que, al igual que en base diez, el añadir ceros a la izquierda de un número binario entero no altera el valor de éste. El mismo número representa 0001101B que 01101B o 1101B. El siguiente programa le ahorrará la tediosa tarea de la conversión a binario.
10 REM PROGRAMA DE CONVERSION DE DECIMAL A BINARIO 20 LET b$ = "" 30 INPUT "Numero?=";a 40 IF a = 1 THEN PRINT "1" + b$: GO TO 20 50 LET C = INT (a/2) 60 LET b$ = STR$ (a - 2 * c) + b$ 70 LET a = c 80 GO TO 40
El sencillo programa anterior no contempla que el número introducido (A) sea no positivo.
Fracciones en binario
Los números no enteros también admiten representación polinomial. En base diez sabemos que todo número fraccionario entre cero y uno se expresa como el cero seguido de un punto, y a la derecha de este, el dígito de las décimas, centésimas, milésimas, etc. Estos dígitos tienen peso igual a 10-1 (= 0.1), 10-2 (= 0.01), 10-3 (= 0.001), etc. respectivamente. Por ejemplo:
El decimal 0.347 = 3 x 10-1 + 4 x 10-2 + 7 x 10-3 = 0.3 + 0.04 + 0.07. Es decir, tres décimas más cuatro centésimas más siete milésimas.
En base dos, los pesos para los dígitos a la derecha del punto serán: 2-1 (= 1/2), 2-2 (= 1/4), 2-3 (= 1/8), etc. Por ejemplo:
El binario 0.011 =0 x 2-1 + 1 x 22 + 1 x 23 = 1/4 + 1/8 = 3/8 en base diez.
Como vemos, el proceso de conversión de binario a decimal para un número fraccionario entre cero y uno es idéntico al de números enteros, teniendo en cuenta los pesos de los dígitos a la derecha del punto.
Hagamos algunos ejemplos:
101.101B= 1 x 22 + 0 x 21 + 1 x 20 + 1 x 2-1 + 1 x 2-2 + 1 x 2-3 = 4 + 1 + 1/2 + 1/4 + 1/8 = 5 + 7/8 = 47/8 en base diez.
En el ejemplo anterior obsérvese que 101.111B = 101B + 0.111B, lo que permite, evidentemente, convertirlo a decimal en un solo paso. Como se ve, la regla que expusimos para la conversión de números enteros, sumar los pesos de las posiciones en que haya unos es absolutamente general.
Convirtamos ahora un número fraccionario entre cero y uno de base diez a base dos. Por ejemplo:
El decimal 9.75D = 9D + 0.75D
9D = 1001B.
El proceso que se sigue con la parte fraccionaria es el siguiente: Multiplicamos la parte fraccionaria por dos, tomamos la parte entera resultante y la escribimos a la derecha de la coma. La parte fraccionaria la multiplicamos nuevamente por dos y repetimos la operación anterior hasta que el resultado sea uno exacto.
0.75 x 2 = 1.5 — 1
0.5 x 2 = 1.0 — 1
luego, 0.75D = 0.11B. Por tanto, 9.75D = 1001.11B.
En el ejemplo anterior obtuvimos, tras dos multiplicaciones, la unidad. Normalmente el número de multiplicaciones necesario será grande o incluso infinito. Pruebe a convertir a binario el número decimal 3.6.
3D = 11B
0.6 x 2 = 1.2 — 1
0.2 x 2 = 0.4 — 0
0.4 x 2 = 0.8 — 0
0.8 x 2 = 1.6 — 1
0.6 x 2 = 1.2 — 1
etc.
Luego 3.6D es igual a 11.10011001… es decir, infinitas cifras decimales.
Tratando con números fraccionarios no le servirá la función BIN. No se preocupe por ello, pues el ordenador no almacena los números fraccionarios en la forma que obtuvimos en los anteriores ejemplos.
En el tercero y cuarto artículos de esta serie trataremos sobre la representación interna, en la memoria del Spectrum, de los números enteros y fraccionarios, positivos y negativos.
Por último, los números en base dos pueden manejarse en notación científica de forma similar a como lo hacemos en base diez. Por ejemplo: en base diez 2.357 x 103 = 23.57 x 102 = 0.2357 x 104 = 2357. Es decir, aumentamos o disminuimos en una unidad la potencia de diez al correr el punto una posición hacia la izquierda o derecha respectivamente.
En base dos, análogamente, podemos poner: 1.010 x 23 = 0.1010 x 24 = 10.10 x 23 = 0.00101 x 26 = 1010 = 10100 x 2-1.
El siguiente programa le permitirá convertir un número entero y positivo en base diez a su equivalente en cualquier otra base comprendida entre dos y dieciséis, ambas inclusive.
10 REM PROGRAMA DE CONVERSION DE DECIMAL A CUALQUIER BASE ENTRE 2 Y 16 20 INPUT "base?="; b: IF b < 2 OR b > 16 THEN PRINT "ERROR": GO TO 20 30 LET b$ = "" 40 INPUT "numero?=": a 50 IF a = 0 THEN PRINT b$ 60 LET c = INT (a / b): LET r = a - b * c 70 LET c$ = STR$ (r) 80 IF r > 10 THEN LET c$ = CHR$ (55 + r) 90 LET b$ = c$ + b$ 100 LET a = c 110 GO TO 50